【中学受験の算数】　図形　面積（基礎４）　解説付き・無料プリント問題

2025年10月16日

中学受験の算数　図形　面積（基礎４）

中学受験算数「図形　面積（基礎４）」のプリント問題で、正方形と円を用いた基本問題で、面積公式（正方形＝一辺×一辺、円＝半径×半径×３.１４）と「全体－一部」「和と差」の考え方を練習します

ぜひこのプリント問題をご家庭での学習に役立ててください。

▼ダウンロードはこちらから

▼中学受験対策や難しい問題を解きたいならこちらから

中学受験の算数　図形　面積（基礎４）　解説・回答

上記問題の解説・回答をします。考え方や回答方法などの理解を深めてください。

① 計算

正答

１４.１３㎠

解説

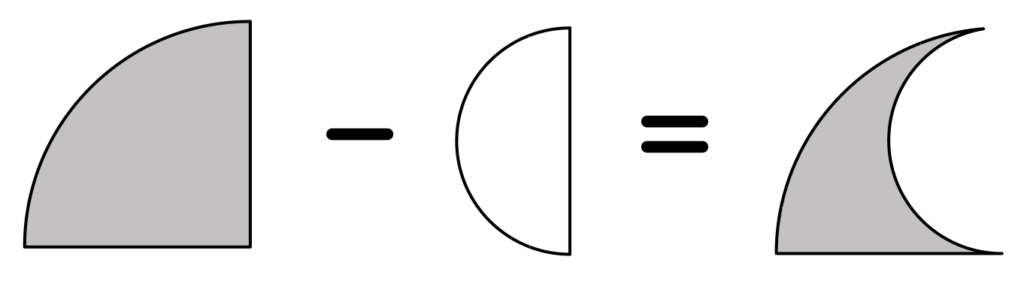
考え方として、上の図のように色のついたおうぎ形から半円を引けば残りの色のついた面積を求めることができる。

まずおうぎ形の面積は、半径が６cmなので、６×６×３.１４➗４＝２８.２６。

次の半円の面積は、３×３×３.１４➗２＝１４.１３。

よって２８.２６ー１４.１３＝１４.１３㎠が正解。

間違えやすいポイント

引き算間違い。

② 計算

正答

１.９３５㎠

解説

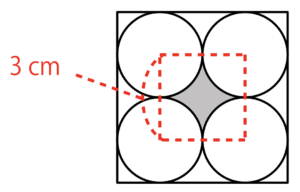
まず上の図のように考える。円の半径が１.５cmなので正方形の１辺は３cmになる。

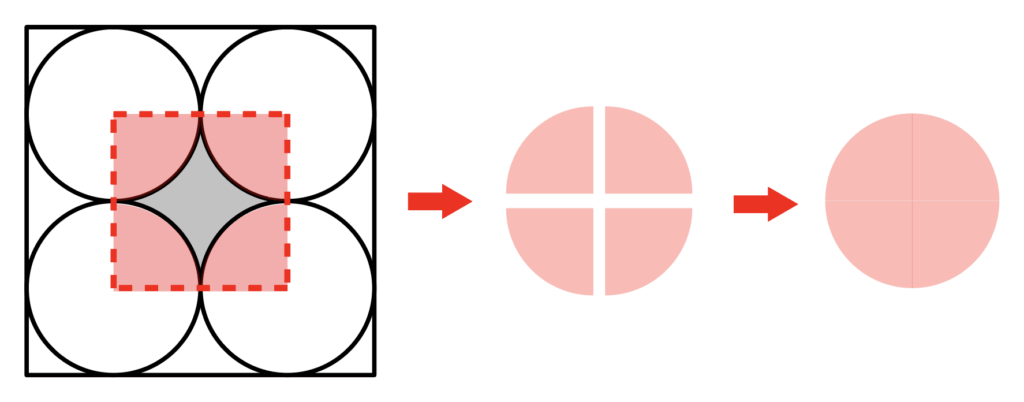
次に上の図のように正方形の中にある1/4のおうぎ形を４つ分、つまりこれは円１つ分になるので、これを正方形から引けば色のついた面積を出すことができる。

まず正方形の面積は３×３＝９。

次に円１つ分の面積は１.５×１.５×３.１４＝７.０６５。

これを正方形の面積から引けば色のついた面積を出すことができる。

よって９ー７.０６５＝１.９３５㎠が正解。

間違えやすいポイント

補助線を引いて正方形に気づかない。

「基礎はできているけど、応用になると手が止まる…」

「中学受験を考えると、プリントだけで大丈夫かな？」

もしこのような不安を持たれているならば、おすすめしたいのが Z会 です。

下の記事で Z会の特徴・評判・どんな子に向いているか を詳しくまとめました。

まずは無料資料請求で検討するのがおすすめです。

▼こちらも合わせて読みたい！